Random Number Generator
A Linear Congruential Random Number Generator (see Numerical Recipies in C by Press, Flannery, Teukolsky, Vetterling, section 7.1. for more information, or just check this link). It goes like this:
S[j] = (A * S[j - 1] + C) modulo M)
R = N * S[j] / M
Where A (multiplier), C (increment), and M (modules) are appropriately
chosen integral constants. S[j] is integral seed which is calculated
from the previous seed (S[j-1]). R is the random double-precision
floating point number calculated from the seed and normalized to the
interval [N,0].
Each program is implemented using symbolic constants for A, C and M. The constants should be:
A = 3877
C = 29574
M = 139968
For an input argument of 1000, the last random number generated should
be 8.163294467 (starting with a seed value of 42).
Test Goal
The test exercises the ability of every language with a pure numerical algorithm, using both integers and floating point operations.
Input argument meaning
The argument specifies the number of random numbers to generate.
Results
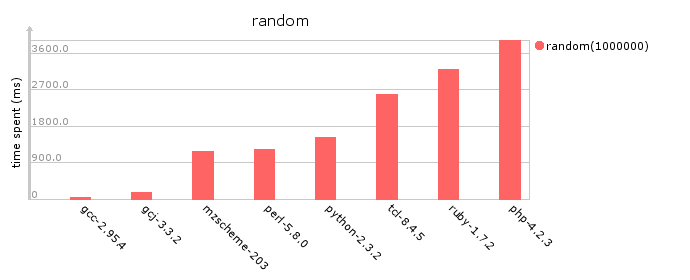

| Language | Milliseconds | Weighted Characters |
|---|---|---|
| gcc 2.95.4 | 27 | 473 |
| gcj 3.3.2 | 164 | 676 |
| MzScheme 203 | 1169 | 506 |
| Perl 5.8.0 | 1218 | 344 |
| Python 2.3.2 | 1533 | 351 |
| Tcl 8.4.5 | 2596 | 531 |
| Ruby 1.7.2 | 3210 | 271 |
| PHP 4.2.3 | 3933 | 400 |
Last updated: Sun Jan 18 11:15:31 CET 2004