ackermann

Ackermann Function

From Harry J. Smith's web page about the Ackermann Function:

The Ackermann function is the simplest example of a well-defined total function which is computable but not primitive recursive. See the article "A function to end all functions" by Gunter Dötzel, Algorithm 2.4, Oct 1991, Pg 16. The function f(x) = A(x, x) grows much faster than polynomials or exponentials. The definition is:

    1. If x = 0 then  A(x, y) = y + 1
    2. If y = 0 then  A(x, y) = A(x-1, 1)
    3. Otherwise,     A(x, y) = A(x-1, A(x, y-1))
    

Test Goal

All the implementations of this test must use recursion. The idea of this test is to measure the performance of highly recursive functions (and indirectly the call stack implementation of the language), with a function with two tail recursive calls, and a non tail recursive call. Tail recursive languages will score better.

Input argument meaning

The argument is used to compute: Ack(3, argument).

Results

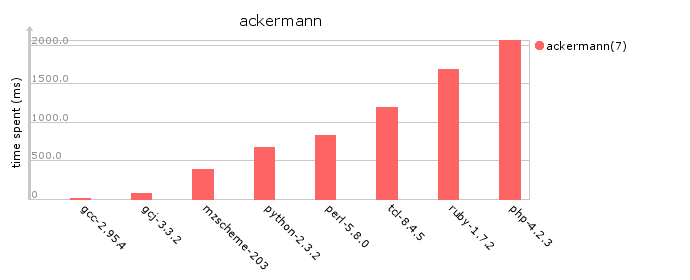
Language	Milliseconds	Weighted Characters
gcc 2.95.4	5	397
gcj 3.3.2	69	341
MzScheme 203	390	394
Python 2.3.2	666	304
Perl 5.8.0	828	271
Tcl 8.4.5	1195	372
Ruby 1.7.2	1690	224
PHP 4.2.3	2067	252

---

Last updated: Sun Jan 18 11:15:31 CET 2004